Dave_89
P
36
Göteborg
Hjälte
667 inlägg
2009-06-15 19:00
Jo det finns en "formel". Det som används är Taylorutveckling. Det går ganska enkelt att visa (genom partiell integration) att en funktion kan skrivas som
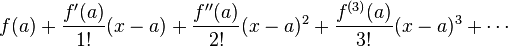
i närheten av en punkt a, med ganska bra noggrannhet.
Det miniräknaren gör är att den Taylorutvecklar och tar med termer tills felet är mindre än någon övre gräns, beroende på hur många värdesiffror som används. Man kan notera att för små x är sin(x) är ungefär lika med x eftersom x>>|x³/3!|.
Taylorutveckling är alltså svaret och speciellt för sinus och cosinus är den

. Testa med några termer i utvecklingen för olika värden på x så ser du att det faktiskt stämmer bra. Taylorutvecklingarna som jag bifogar kallas Maclaurinutvecklingar eftersom de är gjorda i x=0. Maclaurinutveckling är bara ett specialfall av Tayorutveckling.
Tillägg av
Dave_89 2009-06-15 19:24
Det ska poängteras att Taylorutvecklingen är gjord där x mäts i radianer. Detta eftersom derivatan blir mycket trevligare då. Om du vill använda x i grader så är det bara att utnyttja att 180 * [grader] = Pi * [radianer].
Detta är t.ex., Pi/2 [radianer] = 90 [grader], 2 [radianer] = 360/Pi [grader] o.s.v.
Tillägg av
Dave_89 2009-06-15 20:23
Ett andra tillägg är att eftersom utvecklingen här är gjord i x=0 blir den sämre ju större |x| blir. Därför kan det vara en bra idé att reducera x eftersom Sin(x+2Pi)=Sin(x) så att man istället använder ett värde med mindre absolutbelopp. Detta innebär att om vi har t.ex. x=7Pi så blir det Sin(7Pi)=Sin(3*2Pi+Pi)=Sin(Pi) där Sin(Pi) vilket är mycket bättre eftersom Pi ligger närmare 0 än 7Pi gör. Jag är ganska säker på att miniräknaren gör någon typ av reduktion för att få snabbare konvergens hos Taylorutvecklingen.

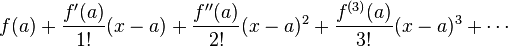 i närheten av en punkt a, med ganska bra noggrannhet.
i närheten av en punkt a, med ganska bra noggrannhet.  . Testa med några termer i utvecklingen för olika värden på x så ser du att det faktiskt stämmer bra. Taylorutvecklingarna som jag bifogar kallas Maclaurinutvecklingar eftersom de är gjorda i x=0. Maclaurinutveckling är bara ett specialfall av Tayorutveckling.
. Testa med några termer i utvecklingen för olika värden på x så ser du att det faktiskt stämmer bra. Taylorutvecklingarna som jag bifogar kallas Maclaurinutvecklingar eftersom de är gjorda i x=0. Maclaurinutveckling är bara ett specialfall av Tayorutveckling.